본문 바로가기
Plant Common Sence/Mechanical

Noise관련 General Information

콩끼리 2013. 1. 20. 02:15

Noise관련 개념


- Sound Intensity

- Sound Power Level

- Sound Pressure Level


1. Sound Intensity


*Sound Intensity는 Sound Power를 면적으로 나눈 값이며, Sound Pressure와 밀접한 관계를 가지나, 동일한 값은 아니다.

 이는 특별히 정의된 양적 개념이며, 단순히 Microphone을 통한 측정은 불가능하다.


 Sound Intensity Level은 아래의 식을 통해 구해진다.

                                 L_\mathrm{I}=10\, \log_{10}\left(\frac{I_1}{I_0}\right)\ \mathrm{dB} \,



2. Sound Power Level


여기서 Sound Power Level이란, 음원에서 나오는 소리가 가지는 "에너지의 양"을 수치화하여 나타낸 것. SWL이라고 줄여 표기하며, 

동일 음원에서의 SWL은 측정 위치와 관계 없이 동일한 값을 가진다.


측정되는 수치는 아주 작은 값이며, 이 작은 수치를 로그를 사용하여 보다 알기 쉽게 나타낸 것을 dB(데시벨)로 정의한다.

SWL은 아래의 수식을 통해 얻을 수 있다.

L_\mathrm{W}=10\, \log_{10}\left(\frac{W}{W_0}\right)\ \mathrm{dB}\,      where     W_0=10^{-12}\ \mathrm{W}=1\ \mathrm{pW}\,



*W0는 보통 10의 -12승의 값으로 설정한다. 아주 작은 값인 1 pico(10의 -12승)를 무소음치로 (0 dB를) 가정하는듯. 



3. Sound Pressure Level *사람이 듣는 것은, Sound Pressure와 직접적인 연관이 있다., Microphone로 츶겅한다.


Sound Pressure Level - Sound Power Level이 Cause라면, Sound Pressure Level 은 Effect이다. 

음파(Sound wave)로 인해 생기는 대기압과의 압력 차, SPL이라고 줄여 표기한다. 내가 알기론 가장 많이 쓰이는 단위 중 하나인 듯.


L_p=10 \log_{10}\left(\frac{{p_{\mathrm{{rms}}}}^2}{{p_{\mathrm{ref}}}^2}\right) =20 \log_{10}\left(\frac{p_{\mathrm{rms}}}{p_{\mathrm{ref}}}\right)\mbox{ dB} ,   ---(1)


일반적으로, Pref의 값은, 20 x 10^(-6) Pa(rms) 가 쓰이며, 사람이 들을 수 있는 가장 작은 소리이다.
 ( 3미터 거리에서 모기의 날갯짓 소리가 가지는 Sound Pressure라고..)



음원이 여러개인 경우,

L_\Sigma = 10\,\cdot\,{\rm log}_{10} \left(\frac{{p_1}^2 + {p_2}^2 + \cdots + {p_n}^2}{{p_{\mathrm{ref}}}^2}\right) = 10\,\cdot\,{\rm log}_{10} \left(\left({\frac{p_1}{p_{\mathrm{ref}}}}\right)^2 + \left({\frac{p_2}{p_{\mathrm{ref}}}}\right)^2 + \cdots + \left({\frac{p_n}{p_{\mathrm{ref}}}}\right)^2\right)

위의 (1)번 식으로부터,  \left({\frac{p_i}{p_{\mathrm{ref}}}}\right)^2 = 10^{\frac{L_i}{10}},\qquad i=1,2,\cdots,n

L_\Sigma = 10\,\cdot\,{\rm log}_{10} \left(10^{\frac{L_1}{10}} + 10^{\frac{L_2}{10}} + \cdots + 10^{\frac{L_n}{10}} \right)\,{\rm dB}
즉, 음원이 여러개인 경우의 SPL은, 각각 음원으로부터의 SPL값들을 ㅣog한 값이다.



SPL과 SWL은 아래와 같은 관계를 가진다.(점음원이라고 가정, 점음원으로부터 측정지점의 거리는 r)

L_\mathrm{W} = L_\mathrm{p}-10\, \log_{10}\left(\frac{1}{4\pi r^2}\right)\,  (음원이 어떤 장애에도 구애받지 않는 위치(free space)에 있을 때)

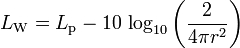L_\mathrm{W} = L_\mathrm{p}-10\, \log_{10}\left(\frac{2}{4\pi r^2}\right)\, (음원이 바닥위에 놓여있을 때 - 반구형태로 소음을 Generate할 떄.)


저작자표시 비영리 변경금지 (새창열림)

'Plant Common Sence > Mechanical' 카테고리의 다른 글

Filter Beta Ratio  (0) 2016.02.29

'Plant Common Sence/Mechanical' Related Articles

티스토리툴바